This year’s Symposium on Theory of Computing (STOC), held in June in Prague, Czech Republic, accepted three papers by NYU Shanghai Assistant Professor of Computer Science Xue Jie. Since 1969, STOC has been one of the most prestigious conferences in theoretical computer science in the world, covering fundamental advances in algorithms, complexity theory, and theoretical computer science at large.
“We’re incredibly proud to see Professor Xue’s work receive such strong recognition, with three papers accepted in a single year,” said Interim Dean of Computer Science, Data Science, and Engineering Nasir Memon. “This demonstrates the research excellence we strive for at NYU Shanghai.”
Professor Xue’s work spans efficient algorithm design for geometric problems and graphs, introducing both faster algorithms and deeper theoretical understanding.
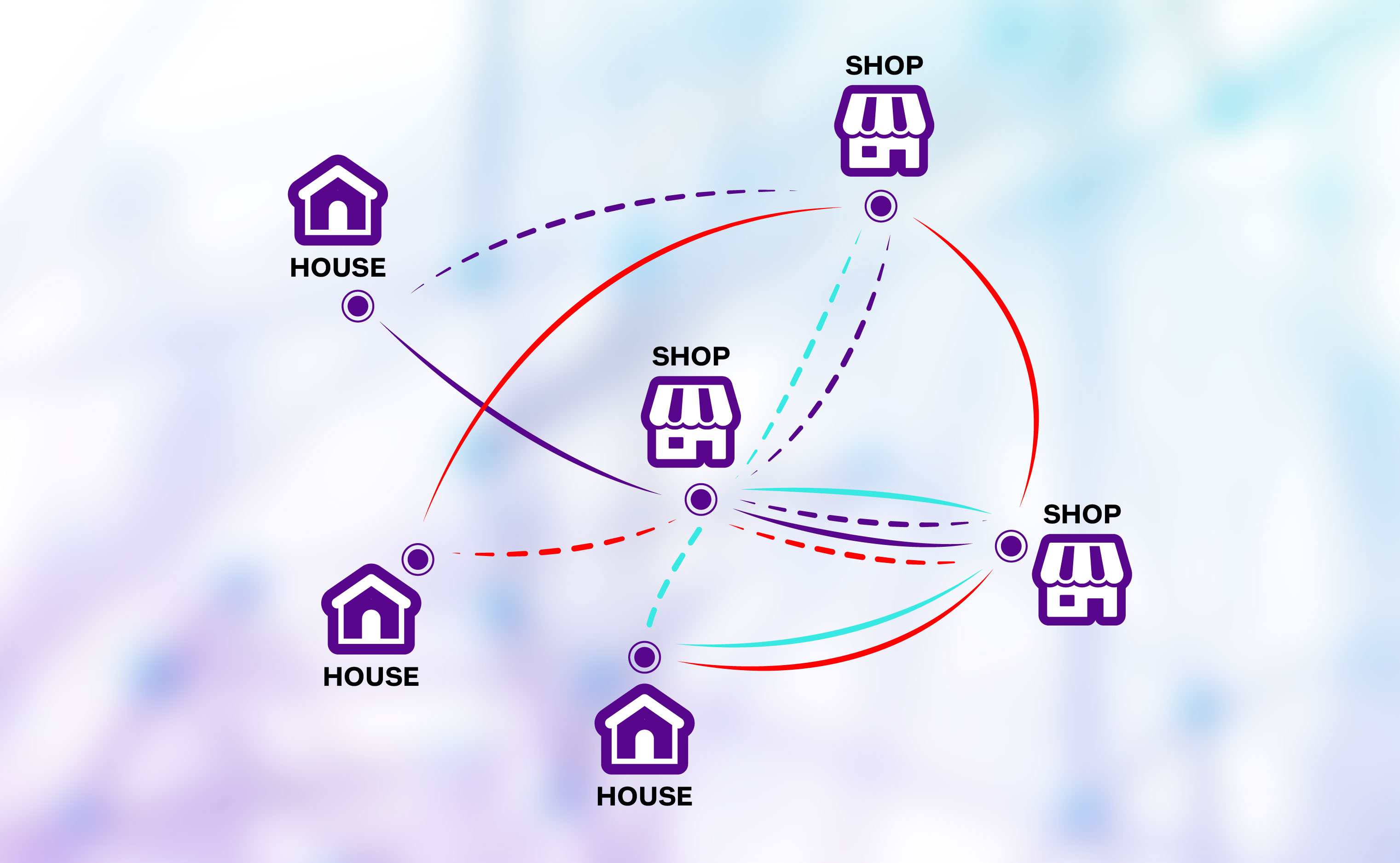
Study 1: Efficient Matching with Minimum Distance
This paper tackles the Geometric Multimatching Problem—how to pair up two sets of points in a Euclidean space while minimizing total connection distance. “Imagine you have houses and stores on a map,” Xue explains. “Each house might need to connect to more than one store (or vice versa), and you want to do this while keeping the total travel distance as small as possible.”
This paper finds two smart and very fast algorithms to solve that matching problem, both of which aim to compute nearly optimal solutions. The algorithms not only work for the Euclidean setting, but also solve the matching problem in more general metric spaces.
Read the paper – Approximation Algorithms for the Geometric Multimatching Problem
Study 2: Fast Detection of Complex Patterns in Sparse Graphs
This paper addresses how to quickly find or count specific patterns in large, sparse graphs, where the patterns of interest are defined via distance constraints between nodes. Think of a huge network (like a social graph or a web of cities). You want to find specific patterns, such as groups of nodes where the pairwise distance is at most 3 and at least 10.
Xue explains: “This paper proposed efficient algorithms to search for or count such patterns in structurally sparse graphs, which significantly improve the computational time of the previous algorithms. In order to design these algorithms, we developed general tools for pattern searching in sparse graphs, which can find applications in other problems as well.”
Read the paper – Efficiently Finding and Counting Patterns with Distance Constraints in Sparse Graphs
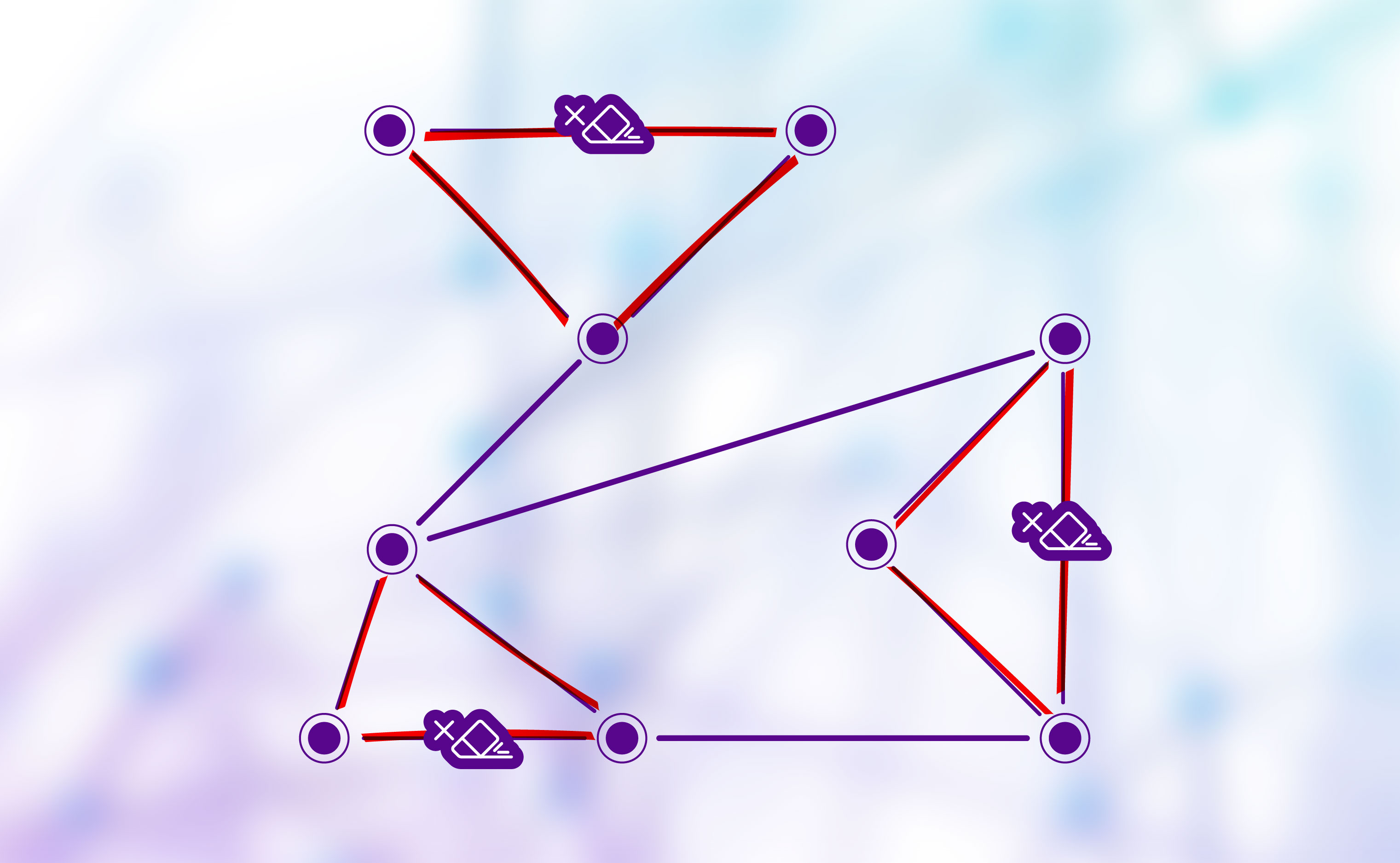
Study 3: Eliminating Problematic Substructures in Graphs
This paper focuses on a class of fundamental problems: how to remove the fewest number of nodes in a given graph to eliminate all unwanted subgraphs (called “forbidden patterns”). These problems are called Subgraph Hitting, and subsume many well-studied graph optimization problems in the literature. The paper essentially proved that Subgraph Hitting can be solved in sub-exponential time as long as the input graph admits small “separators”, a structure whose removal breaks the graph into pieces of balanced sizes. This result significantly generalizes the previous work and deepens the understanding of subgraph-hitting problems.
Read the paper – Subexponential Parameterized Algorithms for Hitting Subgraphs